各位亲爱的读者，近期有读者问我，如何实现数字化行政运营。这个话题有点大，我想从尽我所能的解释在工作中如何应用统计学的知识来展开这个话题，介于学识不足，希望能抛砖引玉，让更多的大咖能参与这个话题。

为了今天这个话题，我计划从以下几个方面来进行探讨：

1、 行政为什么需要数据？

2、 行政需要哪些数据？

3、 获取了这些数据，如何通过统计学的方法将其转化为对决策的支持

首先，行政为什么需要数据？每个人有每个人的想法，每家公司有每家公司的做法，笔者的经验是：

l 通过收集数据，对行政工作进行定量：收益与支出，靠数据说话。

l 通过分析数据，对行政工作进行定性：成果与绩效，靠数据说话。

l 通过可视化数据，让领导明白行政的价值：行政也可以创造价值。

其次，行政需要哪些数据？同理，每家公司的情况不一样，每位行政人的工作习惯也不一样，笔者的经验是：

l 行政日常运营中产生的数据：小到维修耗材的使用情况、厕所耗材使用情况，大到工作变化情况、日常水电煤消耗情况、自动化设备运行数据、餐厅就餐数据、厕所使用频率数据、班车运行数据、资产流转率数据、物料进出库存数据等。

l 与行政工作存在一定关联的数据：比如周边租金情况、打折信息、其他公司行政活动等

l 各类工作中反馈或调研得到数据：比如员工满意度调查数据、餐厅意见反馈数据、第三方满意度调查数据、班车线路满意度调查等

最后，获取了这些数据，如何通过统计学的方法将其转化为对决策的支持呢？我们分享几个具体的做法：

l 利用统计学来获得耗材合理更换的时间：比如说你办公室里面有1000个灯泡，一般的做法是准备个50个灯泡的安全库存的量，然后坏了就更换，坏了就更换。其实还有一种更加高效的办法来管理你的库存。我们还是准备50个灯泡，然后观察这些灯泡在使用中的真实寿命，随后就可以通过统计学的方法，计算出灯泡的预期寿命及接近真实更换频率的有效库存了。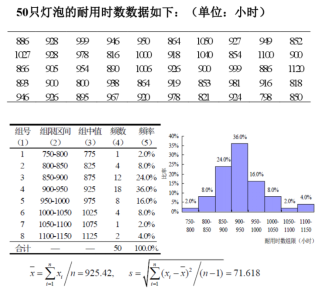

从上面的数据来看，灯泡的有效寿命在925.42小时，误差为±22小时，95%的灯泡使用最小寿命为900.7小时，最大寿命为944.7小时，基于上述的数据，如果我们供应商的供货时间是48小时的话，那亲爱的读者，试着思考一下，这个1000个灯泡的最小化库存设置多少比较合适呢？

l 什么时候结束供冷比较合适？一般是根据天气预报，但是天气预报是个预测，实际上对我们的判断有很大影响，比如笔者之前碰到过为了赶在供暖前清洁空调，根据天气预报安排了清洁空调，结果清洁空调的当天暴热，伙伴们怨声载道。那碰到这样的问题，统计学能帮到我们什么呢？

比如说你计划在11月1日至11月9日的20年同期气温情况，这些数据在气象台的网站上都可以获得。根据历史数据，11月1日至11月9日期间平均有5天高温的日期，而且5次都发生在11月1日及2日。而其他日期的发生概率较小，我们计划在11月3日至11月4日清洁空调，而不在11月1日至2日安排，是否合理呢？

假设高温天在11月1日至11月9日期间发生的，排列为9的9次方，如果高温天仅仅发生在1日和2日，那就是2的9次方，则高温天发生在1日和2日的概率就是2的9次方除以9的9次方，等于0.000132156149335715%，根据小概率原理，你订在11月1日和2日清洁是没有问题的。

l 通过对离散性随机变量的数据分析，获得平均的期望值。

举个简单的例子，班车到站时间是一个不停变化的值，那要在什么范围内到达能够避免乘车人员因为长时间等待而导致的投诉呢？我们可以简单的收集一下数据，比如说：班车是8:40~8:50到达，8：40到达的概率是1/5,8:45分到达的概率是3/5,8:50分到达的概率是1/5，如果乘车人是在8点42分到达候车点的，那他的期望值就是E（X）=3*3/5+8*1/5=3.4，从这个数据上来看，最大的等候时间控制在3.4分钟比较合适。那我们有了数据，就可以计算各个等待时间的比例，然后算出班车到站时间不被投诉的范围了。

l 通过对正态分布的数据恩熙，获得发生问题的概率：

比如说：你需要评估公司设备耗电量是否会超过最大负载呢？以往的做法是根据经验值，进行评估，然后预估的耗电量*设备数量，在实际运用中，会发生这样的预估将存在较大的误差，从而导致用电不足或者申请了多余的电量，那用统计学你要如何计算呢？使用正态分布的方式来计算，首先我们计算一个概率密度，然后计算概率的数学期望即可，具体的计算方式太过学术，大家可以看一下《统计学基础》简单的学习一下即可。

l 利用方差来选择做什么项目

你们部门面临2个需要花钱的项目：增加空调设备和调整厕所设备。这两个项目都和员工满意度息息相关。预期把员工满意度分为优、良、差不同级别，发生概率依次为0.2、0.7、0.1，根据初步调研，你发觉增加空调设备可以提高（X）的满意度和调整厕所可以提高（Y）的满意度，表格如下：（相关数据不是真实数据，请不要纠结，仅仅举例）

那我们应该选择哪个项目做？首先我们来算数学期望值，就是平均提升的满意度。

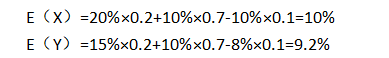
从平均提升的满意度可以看出，2个项目相差不大，从风险方面考虑，下面我们再求出它们各自的方差。

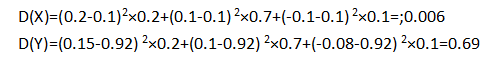
方差越大，说明风险也就越大，虽然两个项目平均提升满意度的概率相近，但是前者的风险明显小于前者。因此，部门应该更倾向于选择风险更小的项目来保证获得满意度的稳定性。

l 利用概率来确认风险发生的概率

比如说，食堂的菜里面有虫子，我们日常的数据显示，一碗菜中出现虫子的概率是0.0004，请问1250个人同时吃饭，吃到虫子的概率有多大？

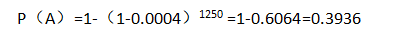
就是39%的概率，既然概率那么大，如果我们无法降低一碗菜中出现虫子的概率的，那我们就可以针对性的制订相关安抚措施。同时，如果我们成功的将虫子出现的概率继续降低的，我们就可以出台很炫酷的奖励抓虫子的制度了。

说了这么多，笔者推荐有意向往行政更高阶层走的读者学习一些简单的统计学。

如果感兴趣的话，可以给笔者留言，笔者会尽力进行回复。当然，笔者也愿意提供有偿的项目咨询服务哦。